📝 Publications
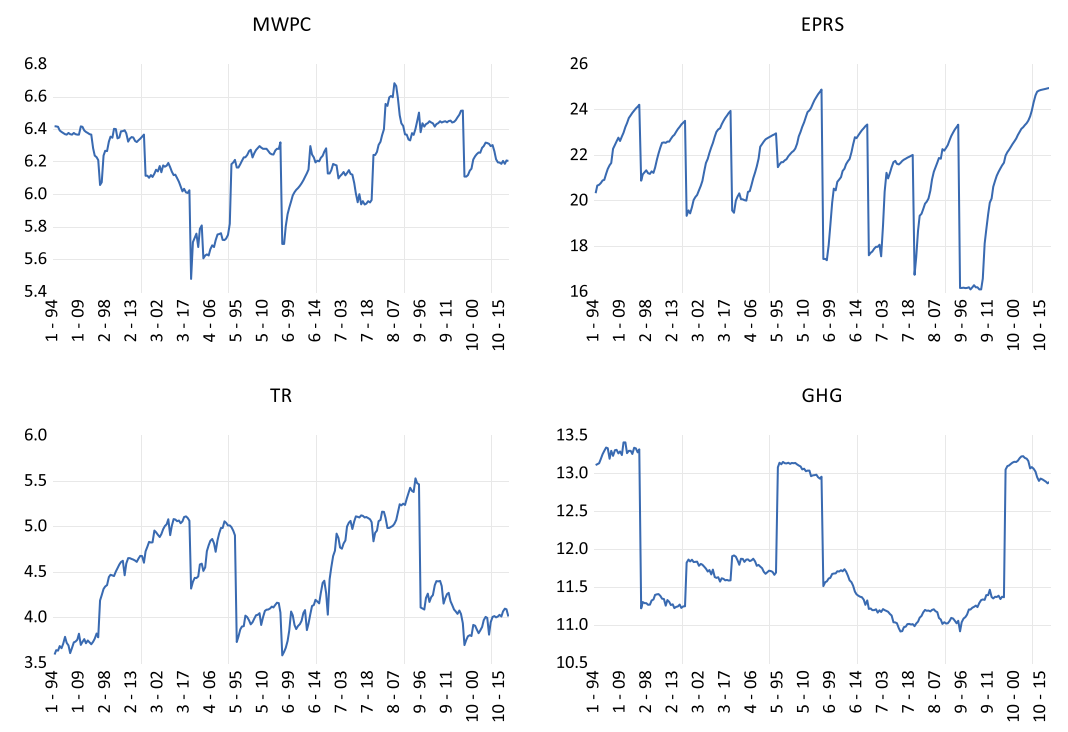
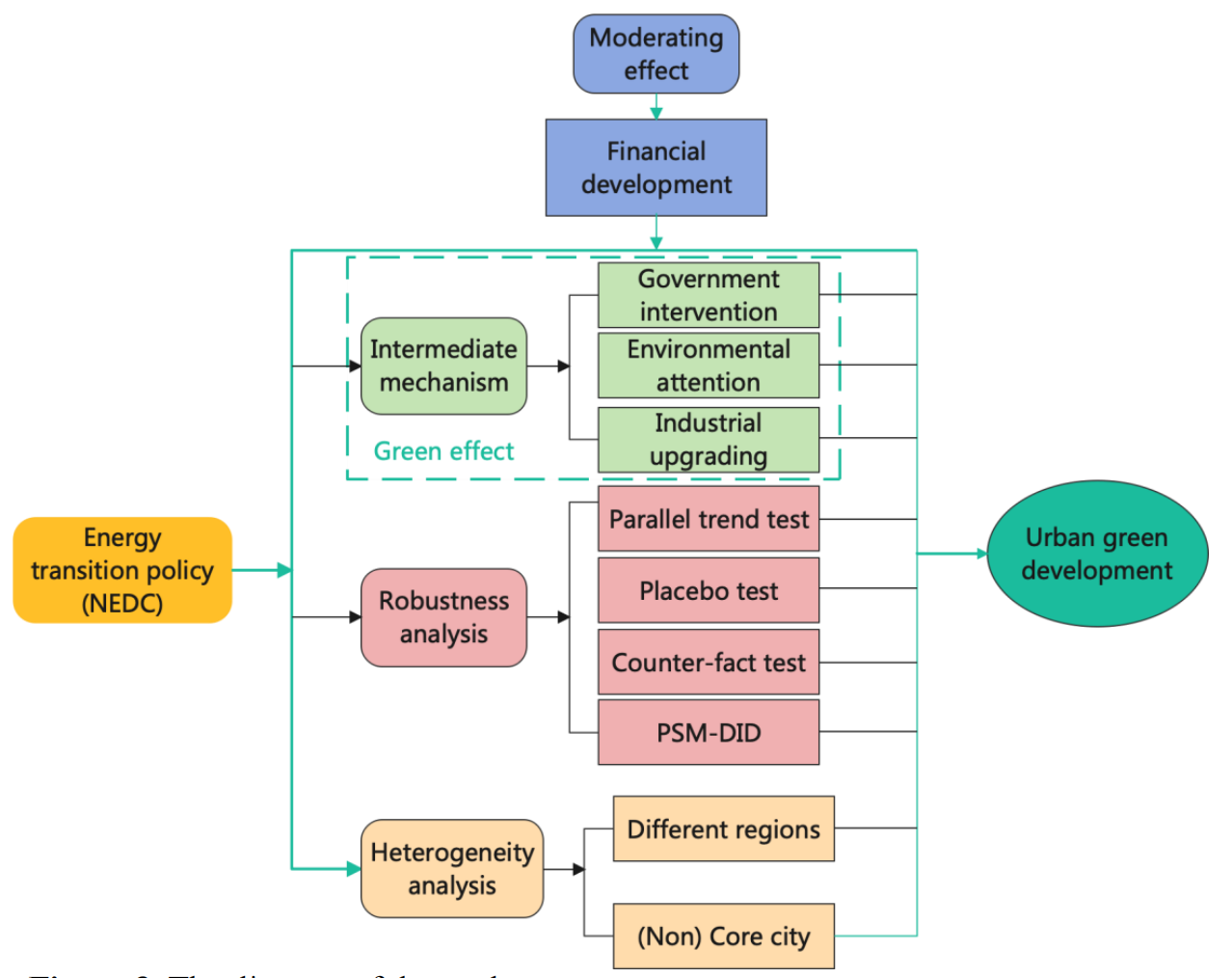
Energy Economics
Computer Vision
Algebra and Representation Theory

The Chinese monoid, denoted as \(Ch_{n}\), is a monoid generated by a totally ordered alphabet \(\mathcal{A}_{n} = \{a_{1} < a_{2} < \cdots < a_{n}\}\) with specific relations \(a_{r}a_{q}a_{p} = a_{r}a_{p}a_{q} = a_{q}a_{r}a_{p}\) for all \(p \leq q \leq r\). This monoid has been studied in the context of growth properties and tropical representations.
This work focuses on tropical representations of \(Ch_{n}\) with and without involution. For each finite \(n \geq 2\), a faithful tropical representation of \(Ch_{n}\) is constructed as a submonoid of the monoid \(UT_{n(n-1)}(\mathbb{T})\) of upper triangular matrices over \(\mathbb{T}\). This representation achieves a smaller dimension compared to previous constructions by Izhakian and Merlet for \(n \geq 4\).
Additionally, a tropical representation of the Chinese monoid with involution is explored. A faithful representation of \((Ch_{n}, \dagger)\) under Schützenberger's involution is provided for each finite \(n \geq 2\), realized as a submonoid of \((UT_{2n(n-1)}(\mathbb{T}),^{D})\), the monoid of upper triangular matrices over \(\mathbb{T}\) under skew transposition.
